はじめに
投資や資産管理、老後の準備について調べていると、さまざまなデータに出会います。
私たちの世代では、高校数学に「統計・解析」という科目がありましたが、この科目は実は投資の世界を理解するうえでも非常に重要な基盤になります。
一般に「統計」は、データを収集・整理し、グラフ化や要約統計を通じて特徴を把握したり、サンプルから母集団の性質を推測することによって、データの傾向を理解しようとする分野です。
一方で「解析」は、得られたデータをもとに、数式的・幾何学的・統計的モデリングを行い、背後にある法則性や因果関係を見出すことを目的とします。
ただし、この2つは厳密に分けて考えるよりも、「データを理解し、説明し、予測する」という一連の流れとして捉える方が自然です。
私は統計解析の専門家ではありませんが、業務の中でデータ群の相関性を調べたり、複数のパラメータから結果を予測する数式を作成したりすることはありました。
その経験から感じるのは、データを正しく読み解くための「統計的な感覚」がいかに重要かということです。
ここでは、投資家にとって基礎となる統計・解析の理解を整理し、最後に応用的な2手法──モンテカルロ・シミュレーション(将来予測)とヒストリカル解析(過去検証)──を紹介します。
平均・中央値・分布の見方
年収や資産額などのデータをざっくり掴むのに有効なのが「平均値」や「中央値」です。
さらにデータの範囲を把握したい場合は、正規分布しているなら「標準偏差」を、そうでない場合は「四分位」などの分布に応じた指標を用います。
投資のリターンは、身長や体重のようにきれいな正規分布にはなりませんが、大まかに毎年のリターンの変動をとらえるのに、標準偏差を用いて「リスクの幅」を定量的に評価できます。
たとえば、平均リターンが5%、標準偏差が6%の投資であれば、
- 約70%の確率で −1%〜+11%
- 約95%の確率で −11%〜+21% の範囲に収まると考えられます。
一方、年収や資産額のようなデータは右に長い裾を持つ歪んだ分布(非正規分布)になりやすいため、四分位を用いて「上位25%」「中央50%」「下位25%」などに分けることで実態をつかみやすくなります。
1. 平均値(Mean)
定義と特徴
(平均値) = (全データの合計) ÷ (データ数)
データが左右対称に分布しているとき(=正規分布の場合)は非常に有効な代表値です。
ただし、分布が偏っている場合には平均値は「実態の中心」からずれてしまいます。
- 正規分布:富士山のように左右対称の形(株式の長期リターンなど)
- 非正規分布:外れ値が多く、平均が引きずられる(年収や資産額など)
論文や研究では「正規性の検定(normality test)」を行う必要がありますが、日常的な分析ではヒストグラムなどの目視判断で十分です。
具体例と使い方
- 株式・債券・REITの平均利回りを比較する際に利用可能
2. 中央値(Median)
定義と特徴
データを小さい順に並べたときの「真ん中の値」。
外れ値の影響を受けにくいため、分布が歪んでいるデータに適しています。
適切な使い方と注意点
- データの多くは正規分布しておらず、平均値では、平均的な値という実像から乖離することがあり、中央値のほうが実像と一致することが多い。
- 最もありがちな結果を把握するのに向く
- 暗号資産や新興国株のように変動が激しいデータに有効
- ただし、中央値だけでは最悪シナリオを見落とす可能性あり
3. 標準偏差(Standard Deviation)
定義と意味
リターンの「ばらつき」を表す指標。
投資の世界では「リスク」とほぼ同義に扱われます。
σ = √( (1/n) Σ (xi − x̄)² )
具体例
- S&P500(過去10年):15〜20%
- 日本国債(過去10年):2〜3%
→ 株式は変動が大きく、国債は安定している。
注意点
- 正規分布を前提にしているため、実際の「極端な暴落(ファットテール)」は反映されにくい。
- 上下非対称のリスクを表すにはVaRなど別の手法が必要。
4. 四分位(Quartiles)
定義
データを4つの等しい部分に区切る値。
- Q1:下位25%
- Q2:中央値
- Q3:上位25%
具体例
ある投資信託の1年リターン:
- Q1 = −8%
- Q2 = +4%
- Q3 = +12%
→ 「下位25%の投資家は−8%以上損し、上位25%は+12%以上得ている」と解釈できます。
活用と注意点
- ボックスプロットで複数資産を比較するときに有効
- サンプル数が少ない場合や極端に歪んだ分布では注意が必要
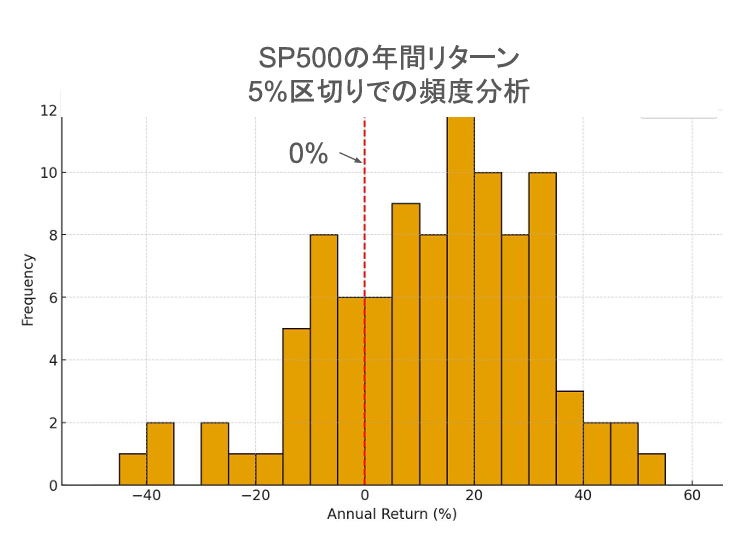
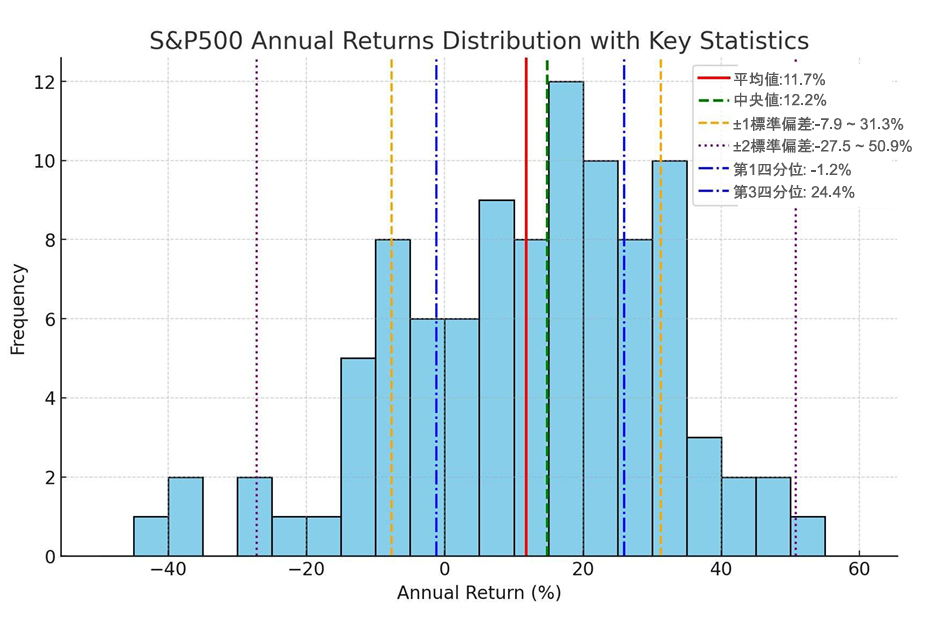
- 赤線:平均値(約 11.7 %)
- 緑線:中央値(約 12.2 %)
- オレンジ破線:±1標準偏差範囲(−7.9 % 〜 31.3 %)
- 紫点線:±2標準偏差範囲(−27.5 % 〜 50.9 %)
- 青一点鎖線:第1・第3四分位(3.6 % 〜 24.4 %)
プラス側にやや偏った分布で、S&P500のリターンが平均10〜12%程度である一方、−20%以上の下落年も一定頻度で発生することが視覚的に確認できます。
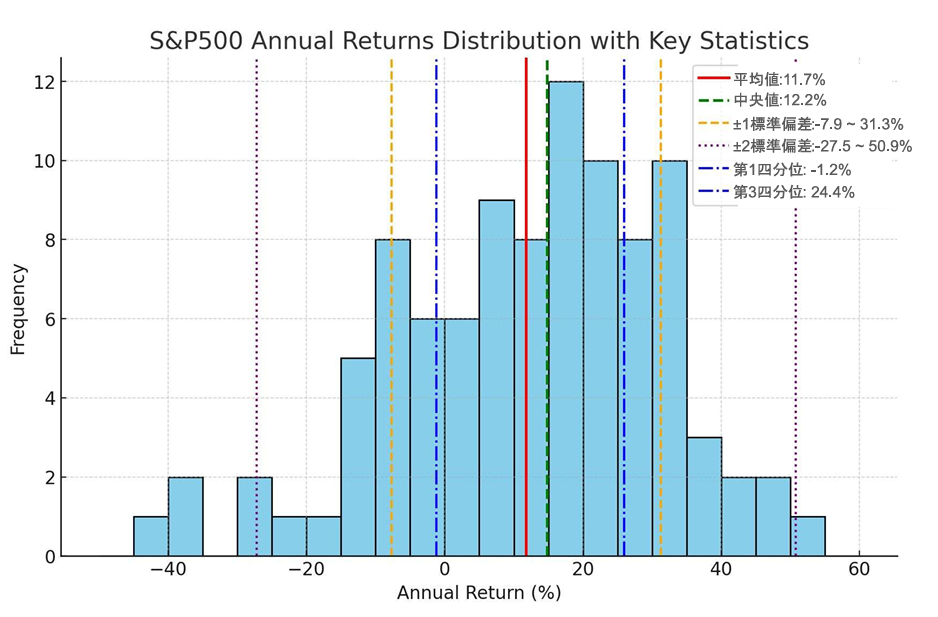
SP500の過去100年から、50年に変更すると正規分布からはかなり外れた感じになりますが、41年間プラスで、9年のみマイナスで、中央値も15.9%となります。 これをそれなりに安定していていいじゃないかと思うか、いやいや悲劇的なマイナスになることもそれなりにあるじゃないかと思うかは、個人のリスク許容度によると思います。
5. 多変量解析(Multivariate Analysis)
単変量解析(平均・分散など)では1つの変数しか扱いませんが、現実のデータは複数の要因が絡み合っています。
その複数の変数を同時に扱い、関係性や影響度を調べるのが多変量解析です。
本来は数学的な知識が必要ですが、さしあたっては、エクセルでも計算可能ですし、私は専用ソフトのJMPを使っていました。
主な手法
- 相関分析 株式と債券の相関は −0.2、株式とREITは +0.7
→ アセットロケーションにおける資産の分散効果の度合いを把握。
アセットアロケーションとは|資産運用の基礎とリスク許容度の見極め方 - 回帰分析 株式リターンを「金利・インフレ率・GDP成長率」で説明。
- 主成分分析(PCA) 多数の銘柄の動きを「市場要因」と「業種要因」に分解。
実務的な使い方
- ポートフォリオの分散効果を定量化
- 相関の低い資産を組み合わせることで、リスクを抑制
相関係数と決定係数(R²)
相関係数(r)
2つのデータがどの程度同じ方向に動くかを示す指標。
- 範囲:−1 ~ +1
- +1:完全に同方向
- 0:無関係
- −1:完全に逆方向
相関が低い、または負の相関がある資産を組み合わせると、リスク分散効果が高まります。
リターンで相関をとる理由
価格ではなく「前日比・週次比・月次比」などのリターンを使うことで、
トレンドの影響を排除し、純粋な動きの連動性を測ることができます。
相関の確からしさを評価する
- 有意性検定(p値) p < 0.05 なら「統計的に有意な相関あり」
- 信頼区間(Confidence Interval) 例:r = 0.5 [95%CI: 0.10–0.75] → 実際の相関がこの範囲にある確率が高い
決定係数(R²)
R² = r²
「Yの変動のうち、Xによって説明できる割合」を表します。
例:
- r = 0.5 → R² = 0.25(25%を説明)
- r = −0.8 → R² = 0.64(64%を説明、方向は逆でも強い関係)
| 指標 | 意味 | 分散投資への示唆 |
|---|---|---|
| 相関係数 r | 値動きの方向性 | 小さいほど良い |
| 決定係数 R² | 説明力 | 小さいほど分散効果が高い |
注意点
- 相関は一定ではない(危機時には上昇しやすい)
- ピアソン相関は直線的関係しか捉えられない
- リスク(ボラティリティ)と併せて考える必要がある
参考:将来と過去を扱う2つの手法
A. モンテカルロ・シミュレーション
- 統計モデルを使い、ランダム試行を多数行って将来を確率分布で描く手法。
- 例:100万円を30年運用(平均6%、標準偏差15%) → 中央値570万円、5%下位150万円、95%上位1800万円
活用:老後資金の持続可能性や「4%ルール」の妥当性検証
注意:前提条件で結果が大きく変わる。未来予測ではなく「幅の理解」のための道具。
資産形成としては、三菱UFJ証券で利用可能
B. ヒストリカルデータ解析
- 実際の市場データをもとにリターン・リスク・相関を検証する手法。
- 例: 世界恐慌 −80%、リーマンショック −57%、株と国債の相関 −0.2〜+0.3
活用:最大ドローダウンや危機時の挙動を把握
注意:「過去は未来を保証しない」が、リスクの現実的な感触を得られる。
代表的な研究として、トリニティ研究がある。 “Retirement Spending: Choosing a Sustainable Withdrawal Rate” Philip L. Cooley, Carl M. Hubbard, and Daniel T. WalzAAII Journal (American Association of Individual Investors), February 1998
おわりに
統計や解析は、投資の「不確実性」を数値として受け止めるための言語です。
完璧な予測をするためのものではなく、「どのくらいの幅で結果がぶれるのか」を理解することが目的です。
データを鵜呑みにせず、分布や相関の背景を考える──
これが、投資家としてより現実的にリスクと向き合う第一歩だと思います。

